Fracture of amorphous materials and composites

To model processes at atomistic scale with high accuracy, particle-based simulation tools as Molecular Dynamics (MD) have been established. In the spirit of “ab initio” approaches, MD is a promising means to model fracture based on the elementary interactions between atoms and molecules. In this regard, it can potentially provide constitutive relations hard to access or even not available from mechanical testing. However, a pure particle-based description becomes computationally prohibitive for system sizes relevant in engineering, particularly in the case of polymers which typically exhibit comparatively large process zones in the vicinity of the crack tip. To tackle this, only e.g. the crack tip shall be resolved to the level of atoms or, if a coarse-grained approach is used, of superatoms.

Hence, multiscale techniques seem to be a promising tool. Several of concurrent multiscale schemes have been proposed and applied to various problems [1,2], but most of them are limited to crystalline materials or highly simplified problems. By implication, a tool specifically designed for multiscale simulation of fracture in amorphous materials is current work in progress in the Capriccio group (see Figure 1). Here, we are considering crack initiation, development, and propagation for various materials as, e.g., inorganic glasses or thermoplastic polymers.

Figure 1: Crack at MD level embedded into an FE domain propagating through through the material: Fracture of silica glass at atomistic resolution; by Felix Weber (M. Sc.)

Adaptivity of the Capriccio method

To decrease the computational effort when a crack propagates through the material, we extend the multiscale Capriccio method [3-6] to adaptive particle regions moving within the continuum. With such a tool at hand, only the vicinity of a crack tip propagating through the material during fracture has to be described at molecular level, whereas the remaining parts may be treated continuum-based with significantly less computational effort.

To resolve the crack tip by MD at its current position, an MD calculation must be activated if a certain load threshold is reached. For this purpose, an MD system must be predeformed according to the instantaneous deformation state. By utilizing a hybrid molecular dynamics-continuum mechanical technique recently proposed by our group [7], the efficiency of the corresponding MD computation can be increased markedly. Upon switching back to FE when crack tip has moved forward and the load threshold is undercut again, the deformation state is transferred to the continuum by employing the Murdoch-Hardy procedure [10].

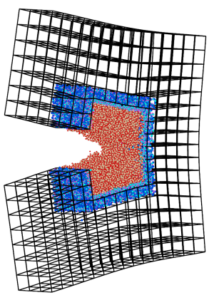
Figure 2: Capriccio simulation of mode I fracture of silica glass: Pure atomistic domain (red) coupled to a finite element region (black) via the bridging domain (blue), by Felix Weber (M. Sc.)

Fracture simulations

In [9,10], we have presented MD-FE coupled fracture simulations using the Capriccio method and obtained promising results. One essential prerequisite is that the MD framework covers bond rupture in an appropriate manner [10,11] (see also Particle-based material description). The study of necessary system and notch sizes is ongoing work.

Further aspects on composite fracture

One of the most challenging fields of research is the investigation of mechanisms in nanocomposites which improve the fracture toughness, even at very low filler contents [12]. Several failure processes may occur like crack pinning, bi-furcation, deflections, and separations [13]. However, these processes take place at very small scales and are thus hardly accessible by mechanical testing. Since the nanofiller particles’ size is comparable to the typical dimensions of the monomers of the polymer chains and thus processes happen at the level of atoms and molecules, continuum-based descriptions and fracture mechanical characteristics are not straightforward to obtain. Again, the Capriccio framework comes into play to link atomistic and continuum descriptions.

–Christof Bauer (M. Sc.) and Felix Weber (M. Sc.)

[1] R. E. Miller and E. B. Tadmor, “A unified framework and performance benchmark of fourteen multiscale atomistic/continuum coupling methods”, Modelling and Simulation in Materials Science and Engineering, vol. 17, p. 053001, 2009

[2] P. T. Bauman, J. T. Oden and S. Prudhomme, “Adaptive multiscale modeling of polymeric materials with Arlequin coupling and Goals algorithms”, Computer Methods in Applied Mechanics and Engineering, vol. 198, pp. 799-818, 2009

[3] S. Pfaller, “Multiscale Simulation of Polymers”, PhD thesis, Erlangen, 2015

[4] S. Pfaller, M. Rahimi, G. Possart, P. Steinmann, F. Müller-Plathe and M. C. Böhm, “An Arlequin-based method to couple molecular dynamics and finite element simulations of amorphous polymers and nanocomposites”, Computer Methods in Applied Mechanics and Engineering, vol. 260, pp. 109-129, 2013

[5] S. Pfaller, A. Kergaßner and P. Steinmann, “Optimisation of the Capriccio Method to Couple Particle- and Continuum-Based Simulations of Polymers”, Multiscale Science and Engineering, vol. 1, pp. 318-333, 2019

[6] W. Zhao, P. Steinmann, S. Pfaller, “A particle-continuum coupling method for multiscale simulations of viscoelastic–viscoplastic amorphous glassy polymers”, International Journal for Numerical Methods in Engineering, vol. 122(24), pp. 7431-7451, 2021

[7] C. Bauer, M. Ries and S. Pfaller, “Accelerating molecular dynamics simulations by a hybrid molecular dynamics-continuum mechanical approach”, Soft Materials, vol. 20, pp. 428-443, 2022

[8] R. J. Hardy, “Formulas for determining local properties in molecular-dynamics simulations: Shock waves”, The Journal of Chemical Physics, vol. 76, pp. 622-628, 1982

[9] W. Zhao and S. Pfaller, “A concurrent MD-FE coupling method towards simulations of fracture of thermoplastic polymers”, Proceedings of XVI International Conference on Computational Plasticity. Fundamentals and Applications 2021, submitted manuscript

[10] W. Zhao, Y. Jain, F. Müller-Plathe, P. Steinmann and S. Pfaller, “Investigating fracture mechanisms in glassy polymers using coupled particle-continuum simulations”, Journal of the Mechanics and Physics of Solids, vol. 193, p. 105884, 2024

[11] F. Weber, V. Dötschel, P. Steinmann, S. Pfaller, M. Ries, “Evaluating the impact of filler size and filler content on the stiffness, strength, and toughness of polymer nanocomposites using coarse-grained molecular dynamics”, Engineering Fracture Mechanics, vol. 307, p. 110270, 2024

[12] M. H. Wichmann, K. Schulte and H. D. Wagner, “On nanocomposite toughness”, Composites Science and Technology, vol. 68, pp. 329-331, 2008

[13] S. Chandrasekaran, N. Sato, F. Tölle, R. Mülhaupt, B. Fiedler and K. Schulte, “Fracture toughness and failure mechanism of graphene based epoxy composites”, Composites Science and Technology, vol. 97, pp. 90-99, 2014

Milestones

Acceleration of molecular dynamics simulations:
Bauer, C.; Ries, M.; Pfaller, S.: Accelerating molecular dynamics simulations by a hybrid molecular dynamics-continuum mechanical approach. Soft Materials, 20, 428-443 (2022). https://doi.org/10.1080/1539445X.2022.2061513.
Fracture simulations of glassy polymers using the Capriccio method:
i) Zhao, W.; Pfaller, S.: A concurrent MD-FE coupling method towards simulations of fracture of thermoplastic polymers. Proceedings of XVI International Conference on Computational Plasticity. Fundamentals and Applications 2021, submitted manuscript.
ii) Zhao, W.; Jain, Y.; Steinmann, P.; Pfaller, S.: Investigating fracture mechanisms in glassy polymers using coupled particle-continuum simulations. Journal of the Mechanics and Physics of Solids, 193, 105884 (2024). https://doi.org/10.1016/j.jmps.2024.105884.
Study of fracture in polymer nanocomposites using pure molecular dynamics:
Weber, F.; Dötschel, V.; Steinmann, P.; Pfaller, S.; Ries, M.: Evaluating the impact of filler size and filler content on the stiffness, strength, and toughness of polymer nanocomposites using coarse-grained molecular dynamics. Engineering Fracture Mechanics, 307, 110270 (2024). https://doi.org/10.1016/j.engfracmech.2024.110270.